
Lois de probabilités
Nous allons nous intéresser à des familles de fonctions réelles (f) très spéciales.

Une loi de probabilité est un
MODELE représentant "au mieux", une distribution de fréquences d'une variable aléatoire.Une classification des lois. On distingue :
Comme l'étude de ces lois n'est pas simple, n'étudierons-nous que quelques-unes d'entre elles.
• Pour chacune d'elles il faut connaître :
•
Dans le cas discret, il faut pouvoir calculer les nombres :Prob(X=k)
•
Dans les cas continus les nombres :![]()
La fonction de densité sera notée f(x), la fonction de répartition F(x)
Exemples de lois "discrètes"
I. Loi UNIFORME
X est une variable aléatoire qui prend les valeurs x1, x2, …, xn avec les probabilités
II. Loi de BERNOULLI
Dans un tel schéma, les épreuves satisfont aux conditions suivantes :
III. Loi BINOMIALE
Le nombre de succès au cours d'une série de n épreuves répondant à un schéma de Bernoulli est une variable aléatoire discrète, appelée loi Binomiale
Conditions:
Echantillon de taille n , 2 issues à chaque tirage de probabilité p et 1-p, Indépendance des tirages.
![]()
Remarques:
![]()
Une relation pratique:
![]()
Exercice
La probabilité pour qu’un tireur atteigne une cible est 1/3.
•
Sachant qu’il tire 5 fois, quelle est la probabilité pour qu’il atteigne la cible au moins deux fois?•
Combien de fois doit-il tirer pour que la probabilité d’atteindre au moins une fois la cible soit plus grande que 0,9 ?Réponses :
- P(X≥2)= 131/243
- n=6
IV. Loi de POISSON
La Loi de densité ou de répartition est donnée par la fonction :
![]()
La loi de POISSON est une bonne approximation de la loi binomiale lorsque p est " très petit " (de l’ordre de 1/100 par exemple)ou p " voisin de 1 " et n " grand " .(n≥20 et p<1/30)
P(X=k) donne la fréquence des valeurs égale à k pour une loi normale réduite.
m=np
n nombre d’épreuves
la moyenne est m, la variance est m.
• Si n " grand ", et p non voisin de 0 ou 1 alors
![]()
Exemples de lois "continues"
I. Loi de LAPLACE-GAUSS
Loi normale de densité ou de répartition est donnée par la fonction :
![]()
f(z) donne l’effectif d’une variable quantitative continue qui suit la loi normale réduite N(0,1)
F(z) donne la fréquence des valeurs inférieures ou égales à z pour une loi normale réduite.
![]()
![]()
Une série ![]() :(
:(![]() ) se transforme en une série
) se transforme en une série ![]() : (
: (![]() )
)
Ce qui permettra d’utiliser les tables de la loi normale réduite
Théorème:
Si
la série ![]() a pour moyenne m et pour écart type
a pour moyenne m et pour écart type ![]() alors on démontre
alors on démontre
que
la série ![]() a pour moyenne 0 et pour écart type 1
a pour moyenne 0 et pour écart type 1
Théorème
:La loi de LAPLACE-GAUSS ![]() est une approximation satisfaisante de la loi BINOMIALE
est une approximation satisfaisante de la loi BINOMIALE ![]() lorsque les conditions suivantes sont satisfaites : n≥30 et 0,2<p<0,8
lorsque les conditions suivantes sont satisfaites : n≥30 et 0,2<p<0,8
Exercice n° 1 :
Une population est composée de 45 % d'hommes et de 55 % de femmes.
On suppose que 4 % des hommes et 0,5 % des femmes sont daltoniens.
On choisit une personne au hasard.
a. Quelle est la probabilité qu'elle soit daltonienne ?
b. Quelle est la probabilité qu'elle soit un homme sachant qu'elle est daltonienne ?
Appelons D l'événement : la personne est daltonienne, et H l'événement, la personne est un homme.

Exercice n° 2 :
On suppose que 2 % des êtres humains en moyenne sont gauchers. Calculez la probabilité pour que parmi 100 personnes, 3 ou plus soient des gauchers.
Réponses :
p=2/100=0,02 n=100 d’où m=2
P(X<3)=P(X=0)+ P(X=1)+ P(X=2) =0,1353+0,2707+0,2027=0,6767
d’où P(X≥3)=1-0,6767=0,3233 =32,3%
**Exercice n° 3 :
On suppose que dans un livre de 200 pages, 220 erreurs d’impression sont distribuées au hasard.
Calculez la probabilité pour qu’une page donnée contienne :
• 0 erreur
• 1 erreur
• 2 erreurs
• 2 erreurs ou plus
Réponses :
La difficulté de l’exercice provient de la difficulté de définir, n, m et p
m=220/200=1,1
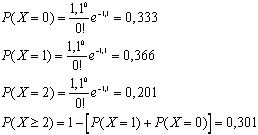
**Exercice n° 4 :
Dans une chaîne de fabrication, 3 % des pièces sont défectueuses.
On prélève une pièce, on examine si elle est défectueuse et on la replace parmi les autres.
On répète 120 fois cette expérience.
Quelle est la probabilité pour qu’on ait 5 pièces défectueuses ?
Réponses :
--> p=0,03 et n=120 d’où m=np=3,6
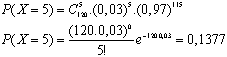
**Exercice n° 5 :
Un représentant de commerce doit visiter 40 clients distincts.
Chacune de ces visites est indépendante des autres. Quelle que soit la visite considérée, la probabilité de l’événement : " le représentant rencontre le client " est égale à 0,6.
Calculez les probabilités suivantes :
A: aucun client n’est rencontré
B: un client au moins est rencontré
C: tous les clients sont rencontrés
Réponses :
Comme n " grand " , p " non voisin de 0 ou 1 ", on peut utiliser une approximation par la loi de Laplace-Gauss. m=0,6*40=24, p=0,6 q=0,4 l’écart type est égal à 3,1
• Prob(A) voisin de 0 z=-7,75
• Prob(B)voisin de 1
• Prob(C)voisin de 0 z=5,16