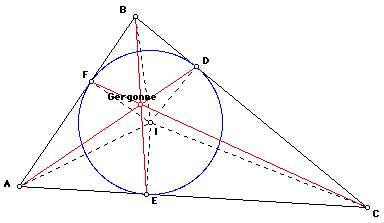
Le point de Joseph Gergonne (1771-1859)

 

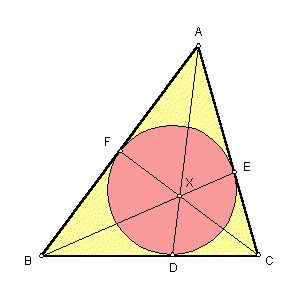
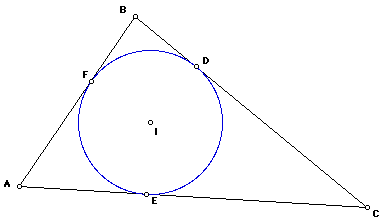
Soit un triangle ABC admettant le point I comme centre du cercle inscrit.

Ce cercle inscrit est tangent aux côtés AC, BC et AB respectivement aux points E, D et F.

 

 

 

 

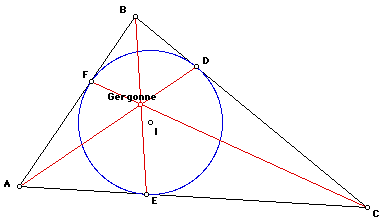
Le Point de Gergonne est le point de rencontre des segments [AD], [BE], et [CF].

 

 

Observez que le point I est sur les bissectrices du triangle ABC et les rayons ID, IE, et IF sont perpendiculaires aux côtés du triangle ABC. De ce fait, trois triangles rectangles isocèles  conguents  existent.

 

Les produits : (AF)(BD)(CE) et (AE)(CD)(BF) sont égaux ( car BF = BD, CD = CE, et AE = AF) donc les rapports de ces nombres est égal à 1. D'après le théorème de Céva, Les trois céviennes du triangle sont concourantes.