A
propos du géoplan 3 X 3
Le géoplan (ou planche à clous) que je
préfère est celui à 9 clous. Il est déjà suffisamment riche pour découvrir le
monde des formes à l'école élémentaire.
Les élèves du cycle 3 pourront construire
leur géoplan à partir d 'une planchette de contreplaqué de dimensions (12
X 12 X 1) (cm). Avoir l'avoir poncé ils chercheront à placer les
clous (en laiton) au bon endroit . Un gabarit est d'une bonne
utilité.
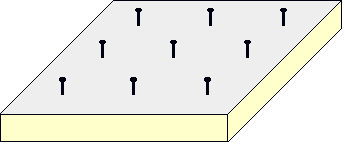
Après un moment de création libre, puis des reproductions
de modèles réalisés avec 1 élastique on entreprendra l'étude du géoplan.
Voyage dans le monde des 9
points
a. Il y a 9 points
que l'on nomme : ![]()
b. Il y a huit
familles de triangles ce qui fait : ... triangles
c. Il y a des
segments. Beaucoup... Classons-les selon leur longueur : ![]()
d. Il y a des
directions ...
e. Il y a des
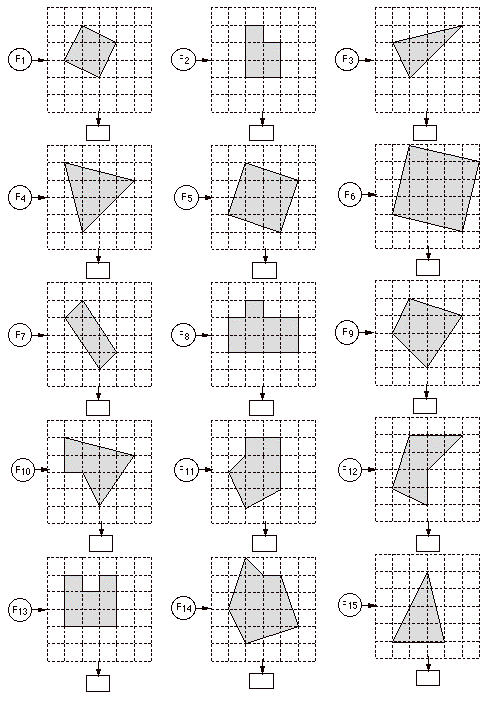
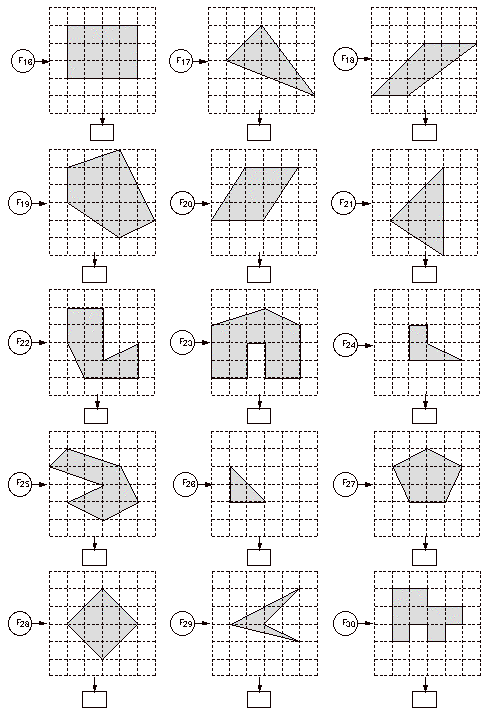
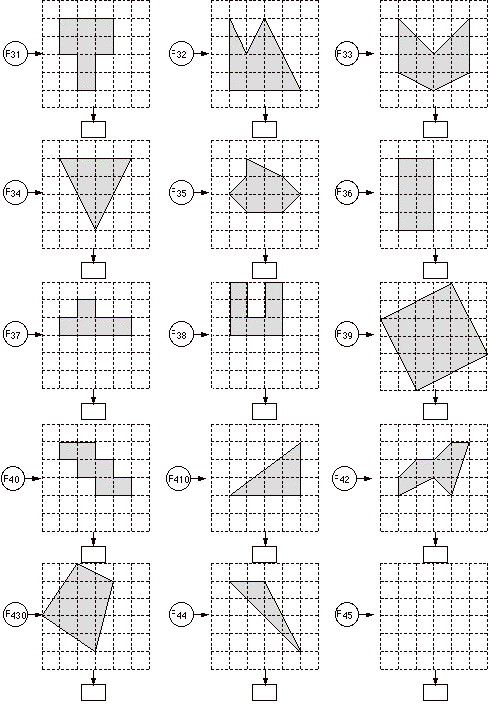
quadrilatères... mais aussi des pentagones,... octogones, nonagones.
f. Travail très
intéressant concernant les aires de polygones.
g. On classe les
quadrilatères selon leurs propriétés.
h.
On peut calculer l'aire des domaines
i.
Voilà rapidement
cités quelques idées d'utilisation en classe.



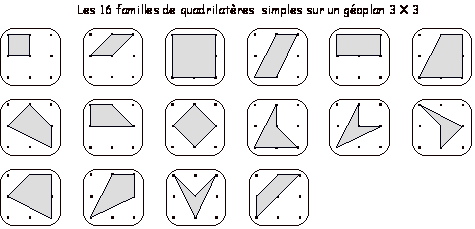
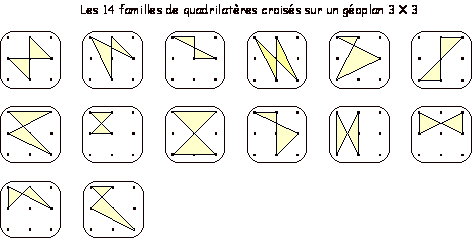
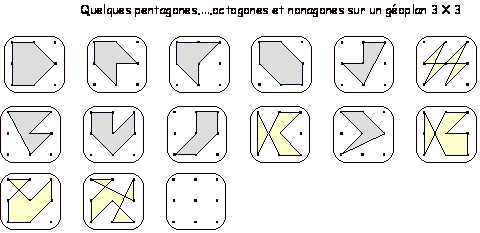
Solutions :
Vous
trouverez 76 triangles dans le monde des 9 points mais aussi 36
segments.
A propos du calcul des
aires de quelques surfaces polygonales
On
choisira par exemple un carré comme ci-dessous comme unité d'aire.

Quatre
méthodes permettront de découvrir l'aire d'autres domaines polygonaux.
Méthode
ní1 : dite des
décompositions
Décomposez
le domaine en domaines dans les aires sont connues
Illustration
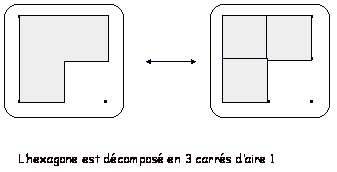
Méthode
ní 2 : dite des
compléments
On
considère le domaine comme partie d'un domaine plus vaste
Illustration

Méthode
ní 3 : dite par
découpage-recollage
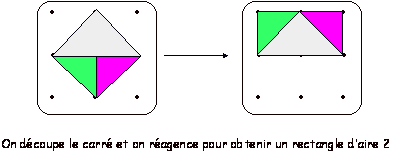
On
découpe le domaine en parties que l'on recolle ailleurs pour obtenir une
figure dont on sait calculer l'aire.
Illustration
Méthode
ní 4 : utilisation de
formules
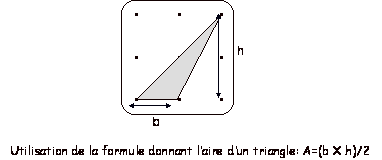
On
applique un formulaire connu
Illustration
Très souvent on combine les
méthodes ci-dessus
Grilles pour la création de formes
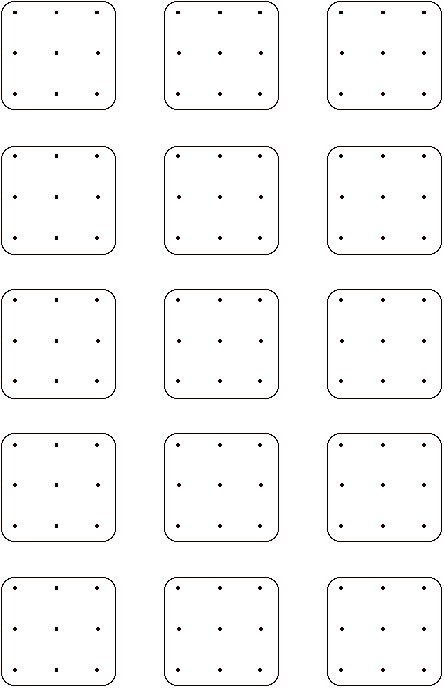

Calculez de différentes manières l'aire de
ces SURFACES