Mathématiques en maternelle
CHAPITRE 1 . Généralités
I. Peut-on parler de mathématiques à l'école maternelle ?
La réponse n'est pas évidente. Si l'on consulte les I.O. concernant l'école maternelle, on ne trouve nulle part de rubrique mathématique. Il existe pourtant toute une littérature sur les mathématiques pour les jeunes enfants (voir la bibliographie donnée en annexe) mais les titres de ces documents sont révélateurs du statut ambigu de cette discipline. Certains parlent :
- d'initiation mathématique
- de situations mathématisables
- de prémathématiques
- de jeux mathématiques
- d'éveil mathématique
- de situations - problèmes d'ordre mathématique
- d' éducation mathématique
-
... et la liste n'est pas close....
Trouvez une réponse à la question suppose que l'on sache ce que sont les mathématiques, qu'est ce qui permet d'attribuer le qualifi–catif "mathématique" à une activité. Redoutable question !
II. Pourquoi des mathématiques à l'école maternelle ?
a. Il semblerait que les mathématiques participent de façon privilégiée au développement de "certaines com–posantes " de "l'intel–ligence" des enfants.
b. Il s'agit de préparer les apprentissages mathématiques futurs.
III. Quelle mathématique à l'école maternelle ?
o Il établit des sériations, c'est à dire ordonne des collections en fonctions de propriétés.
o L'enfant découvre et construit le nombre. Il apprend et récite la comptine numérique.
o Il compare des collections terme à terme.
o Il découvre et construit des relations spatiales (voir I.O p 61)
Les textes officiels n'apportent pas beaucoup d'informations quand au contenu d'ordre mathématique , on peut néanmoins préciser des domaines à propos desquels des activités peuvent être conçues et menées.
- Construction et structuration : "des espaces , du temps, du schéma corporel...
- Formation , développement et utilisation de "langages".
- Développement d'une pensée logique et relationnelle.
- Découverte de quelques "grandeurs mesurables" : le nombre entier, la masse , la longueur, l'aire....
On mettra donc les enfants face à des situations permettant d'aborder des concepts et méthodes dans les do–maines suivants :
A. Construire, structurer, organiser, étudier:
a. les espaces, les formes, les repères, les parcours.
b. le temps.
c. le corps.
B. Développer, utiliser, maîtriser:
a. une pensée symbolique.
b. divers "langages".
C. Sensibiliser à quelques grandeurs mesurables:
a. le nombre entier.
b. la longueur, l'aire, la masse, la capacité...
D. Découvrir et utiliser quelques concepts de base.
a. les propriétés des "objets".
b. les ensembles et sous-ensembles.
c. les relations et en particulier les classements et rangements...
d. les files , suites , arbres et tableaux.
e. la notion d'algorithme.
f. la logique.
La liste des objectifs qui vont suivre ne constitue pas un programme mais doit servir de support à la ré–flexion des maîtres .
E . Structuration de l'espace, du temps et du schéma corporel.
a. Observer, manipuler, nommer, reconnaître, classer, reproduire, agencer des formes.
Savoir:
. regrouper spontanément des objets de même forme ou couleur ...
. reconnaître visuellement ou grâce au toucher des objets.
. désigner par leurs noms quelques formes géométriques simples.
. dessiner ou reproduire à l'aide de gabarits des formes.
. classer les formes suivant un critère donné .
Par exemples: - distinguer lignes ouvertes ou non , simples ou non simples...
. reconnaître et reproduire certaines configurations d'objets.
. réussir des jeux d'agencements, d'encastrements, d'emboîtements .
.
.
b. Se situer, se déplacer dans l'espace. Situer les objets...
Savoir:
. énoncer la position relative d'objets:
- par rapport à soi-même
- les uns par rapports aux autres
- par rapport à un repère standard
. se situer ou situer des objets à l'intérieur, sur la frontière ou à l'extérieur d'un domaine.
. suivre des itinéraires librement ou en suivant des consignes.
. repérer une case , un nœud d'un quadrillage .
. s'orienter et se déplacer vers...
.
.
c. Structuration du corps.
Savoir :
. découvrir les positions relatives des parties du corps.
. nommer diverses parties de son corps.
. mettre en place les axes et plans fondamentaux liés au corps et dégager le vocabulaire qui s'y
rattache.
.
.
d. Structurer le temps :
Savoir :
. structurer la journée, la semaine... (établir des repères: fêtes, événements...)
. structurer une activité , une histoire... ( remettre dans l'ordre une histoire en images, exprimer
oralement la relation qui les unit).
. comparer des durées ( montres, sabliers...)
.
. Formation et développement de "langages".
Savoir:
. utiliser et comprendre le rôle des signes , symboles et pictogrammes.
. traduire par le dessin, la peinture, le modelage et les constructions en volume , les images que
l'enfant porte en lui.
. représenter et verbaliser les situations vécues.
. utiliser arbres diagrammes, tableaux à double entrée, graphes .....
. représenter des collections, des relations...
.
G. Développement d'une pensée pré-logique et relationnelle.
Savoir:
. reconnaître et verbaliser des "propriétés d'objets".
. classer suivant un ou deux critères donnés.
. définir des collections d'objets par la propriété commune des éléments ou en extension.
. distinguer les notions de paires et couples.
. associer des objets appartenant à une ou deux collections de diverses façons
(un à un ,un à plusieurs...)
. utiliser les connecteurs "non" , "et" , "ou" ( négation, conjonction , disjonction de propositions).
.
.
.
H. Approche de quelques grandeurs mesurables.
Savoir:
. Percevoir la grandeur comme propriété attachée à des objets ou collections d'objets.
. comparer des grandeurs directement ou indirectement.
. écrire les premiers nombres.
. maîtriser la "comptine numérique" jusqu'à 30 ?
. comparer numériquement des collections "petites"
. reconnaître globalement de petites configurations
. construire de "petites collections".
. se grouper ou grouper des objets par 2 ou par 3.
. distribuer des objets 1 à 1 ou 2 par 2 ...
. comparer des masses.
.
IV. Comment aborder les activités mathématiques ?
A. Quelques principes de base:
a. Du concret vers l'abstrait ou du vécu vers le conçu.
Les concepts mathématiques sont construits petit à petit par l'enfant à partir des actions.
Il y a lieu de distinguer diverses phases dans l'acquisition d'un concept:
1. phase vécue, manipulatoire , déambulatoire...
- corps, action, mouvement.
2. phase verbale ...
- on parle de ce que l'on fait ou de ce que l'on a fait .
3. phase "idéographique...
- l'enfant procède à des désignations, des représentations ( des objets et des actions) très
proches du concret.
4. phase symbolique...
- on assiste à des épurations successives des représentations précédentes pour arriver à
des représentations abstraites relevant des conventions établies par la classe ou
imposées par le maître.
b. Des approches multiples.
Toute connaissance, tout comportement relève non pas d'une mais de plusieurs expériences non pas iden–tiques mais isomorphes. C'est le double phénomène "assimilation et accommodation" que la connaissance se struc–ture. Un concept s'acquiert d'autant plus facilement qu'on peut le rattacher à des modèles déjà as–similés. Il s'agira de partir de situations-problèmes riches, présentant vrai–ment une ou plusieurs difficul–tés à surmon–ter.
c. Symbolisations progressives et multiples.
L'introduction de "langages" divers facilite le passage du concret vers l'abstrait.
d. Situations motivantes :
Sans motivation (internes ou externes) l'apprentissage se fait mal ou pas du tout. L'importance de l'affectivité a été rappelée par de nombreux psychopédagogues en particulier par Piaget :
" l'affectivité est le moteur ou le frein de l'intelligence".
e. Respect du développement génétique :
Le développement intellectuel de l'enfant passe par divers stades qu'il importe de connaître.
f. Pédagogie globale:
Éducation décloisonnée, s'appuyant souvent sur un vécu global , sur un engagement total de la personnalité.
B. Un problème ouvert.
La maîtresse a le choix entre deux stratégies pédagogiques pour introduire les concepts et
méthodes mathématiques.
1. Travailler par thèmes et attendre que des situations mathématiques se présentent.
2. Rechercher, provoquer (en plaçant les élèves dans un environnement propice) des situations
motivantes pour illustrer des objectifs fixés préalablement.
---> Ma préférence va ( du moins "en section des grands ") à la 2 ème stratégie.
---> En " petite et moyenne section " on peut privilégier la 1 ère stratégie.
C. Durée, place et fréquence des activités mathématiques.
Il est difficile de fixer une durée standard pour une activité. Néanmoins on se souviendra que les capacités d'attention des jeunes enfants sont très limités et s'effritent rapidement.
Dans de nombreuses classes c'est en début d'après-midi que se situe le moment mathématique !
En section des grands un moment mathématique quotidien est souhaitable.
D. Quelques formes d'organisation
a. Le "moment de pédagogie collective.
Se pratique en salle de jeu ou dans un autre endroit privilégié de la salle de classe. Il peut servir:
- à introduire une activité
- à aborder un concept nouveau
- à faire une synthèse d'une activité vécues.
C'est un moment difficile à mener ( surtout si l'effectif est grand) générateur de beaucoup de questions-réponses. Ne pas en abuser surtout en section des "petits".
b. Les moments de pédagogie individuelle.
Se pratique lors d'ateliers, ou au moment de l'accueil. Ils permettent des approches libres, orientées, diffé–renciées, individualisées ou le contrôle.
c. Les "moments" de pédagogie de groupes.
Groupes de niveau, de soutien ou groupes se formant spontanément lors d'activités diverses (jeux par exemples). Manipulations in–dividuelles, travaux écrits.
E. Le rôle de la maîtresse.
Elle devra :
. organiser l'environnement des élèves.
. veiller à ce que chaque enfant se trouve dans un contexte lui permettant de se sentir en sécurité
de sentir que l'on s'occupe de lui.
. se souvenir de l'importance de l'affectif qui joue un rôle moteur fondamental.
. rechercher des situations, des thèmes, préparer le matériel...
. aider les enfants à: préciser leurs projets, les discuter, les communiquer, les comparer..
.
.
CHAPITRE 2. Quelques notions fondamentales
LES ESPACES
I. Généralités :
Cette notion d'espace recouvre les concepts les plus divers suivant que l'on est astronaute, physicien, ma–thématicien, géo–graphe...homme de la rue, ou jeune enfant.
A. Le concept d'espace pour le mathématicien.
Le mathématicien ne peut se contenter d'une simple description de l'espace. Il a besoin d'un modèle. Le mo–dèle le plus ancien est celui d'EUCLIDE ( mathématicien et philosophe du 3 ème siècle avant JC). Il est basé sur les notions de droite, point, angle, lon–gueur...
Depuis de nombreux autres modèles ont vu le jour: espace affine, espace vectoriel, espace de Riemann, ....
Une classification suivant la "dimension" de l'espace :
- l'espace - temps de dimension 4.
- l'espace habituel de dimension 3.
- l' espace de dimension 2.
- l'espace de dimension 1.
Mais n'oublions pas que l'espace dans lequel nous vivons et nous déplaçons :
- est peuplé d'objets divers.
- possède une "certaine structure".
B. Le concept d'espace pour le psycho-généticien.
" La construction de l'espace n'est pas de l'ordre du voir, mais du concevoir. Elle se fait en organisant les ob–jets les uns par rapport aux autres et tous par rapport à un cadre de référence". LEGRAND
Les psycho-généticiens nous apprennent que l'enfant organise peu à peu le monde à partir de son corps et de ses actions. C'est en partant de l'organisation de la connaissance du corps, de cette image cohérente du moi et par référence continuelle à celle-ci qu'il va peu à peu agrandir son espace, investir l'espace envi–ronnant, l'espace des objets et l'espace inter-objets.
L'adulte ne doit donc pas oublier que le concept d'espace n'est pas une donnée innée chez l'enfant mais cons–truite progressivement et que son appréhension se fait successivement sur deux plans :
- le plan sensori-moteur.
Toutes les acquisitions primitives et fondamentales naîtront des activités perceptivo-motrices.
- le plan intellectuel.
On assistera à une modélisation progressive, une conceptualisation de l'espace grâce notamment
à l'élaboration de "langages ( gestuels, oraux , graphiques..)".
.Le passage d'un plan à l'autre selon des modalités et une progression a été finement étudié par
PIAGET et son équipe (voir :” La construction de l'espace " et " La géométrie spontanée " PUF)
-Il dispose pour cela :
. De deux activités motrices essentielles :
a. La préhension :
qui lui permet de saisir, de toucher, de lancer,.... de jeter des objets.
b. La locomotion :
qui va lui permettre d'agrandir considérablement les dimensions de l'espace investi et
qui permet de relativiser et de multiplier les points de vue.
. et des sens :
Les activités motrices sont couplées à des activités perceptives (visuelles, tactiles...).
Les étapes de l'organisation spatiale :
a. Organisation du moi corporel.
b. Situation des objets par rapport au moi.
c. La situation du moi par rapport aux objets.
d. La situation des objets entre eux.
C. Des espaces particuliers.
En " 3- dimensions ":
- l'espace de la classe
- la portion d'espace que je vois
- la portion d'espace qui m'est accessible
- les espaces de jeux , de travail ...
- la trilogie terre-mer-air
-
En " 2- dimensions " :
- le plan
- des portions de surfaces
- l 'espace graphique (ma feuille,...)
-
En " 1- dimension " :
- les lignes
-
II. L'espace des objets :
a. Plusieurs classifications de ces objets sont possibles.
. classifications liées à nos perceptions visuelles, motrices, tactiles...
(couleurs, formes, taille, masse.......)
. classifications liées aux "fonctions" , aux utilisations des objets.
( animaux, objets comestibles....)
.
b. Plusieurs opérations sur ces objets sont possibles.
. manipuler, déplacer, jeter, utiliser...
. observer,....
. agencer,.....
. représenter, décrire, dessiner...
. construire, reconstruire, fabriquer, transformer...
. classer, trier, ranger, organiser, structurer, ordonner, empiler,....
. mesurer,..., repérer....
|
LES FORMES
|
Ce concept est fondamental car présent dans tout ce qui nous accessible par la vue et le toucher. Il est pré–sent dans la nature du ni–veau macroscopique au niveau microscopique (galaxies, plantes, mollusques,... cristaux, ...) ainsi que dans les objets crées par l'homme.
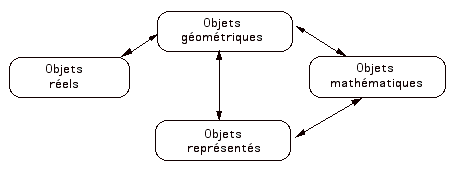
La forme est un attribut (une propriété) des "objets”. Les difficultés proviennent de la grande variété des formes et de l'ambiguïté des "objets”. Les objets sur lesquels on travaille sont toujours quelque part entre "les objets réels” , "les objets géométriques", "les objets représentés" et les "objets mathéma–tiques".
Concept qui est assez difficile à mettre en évidence car présent avec d'autres attributs non essentiels. Il est important de bien choi–sir les objets d'étude afin de bien le mettre en évidence.
Quelques essais de classification des formes.
I. Une classification "dimensionnelle" des formes géométriques.
on distinguera
a. Les formes de dimension 3 ( les solides)
b. Les formes de dimension 2 ( les surfaces)
c. Les formes de dimension 1 ( les lignes)
Il ne faudra pas oublier que des objets de dimension 1 peuvent être plongés dans des espaces de dimension 2 ou 3 , et que des objets de dimension 2 peuvent être plongés dans un espace de dimension 3.
Une sous-classification importante:
II. La classification algébrique des formes géométriques.
Elle résulte de la définition de la relation d'équivalence R suivante sur un univers de formes
Étant donnés :
un ensemble de formes E et un groupe de transformations géométriques (G , o )
F R F' si et seulement si f C ( H, o ) f ( F ) = F'
Si le groupe est :
A - L'ensemble des Homéomorphismes alors les formes seront classées selon des critères topologiques.
B - L'ensemble des Projectivités alors les formes seront classées selon des critères projectifs.
C - L'ensemble des Affinités alors les formes seront classées selon des critères affines.
D - L'ensemble des Similitudes alors les formes seront classées selon des critères semblables.
E - L'ensemble des Isométries alors les formes seront classées selon des critères métriques.
---> Les groupes sont indiqués des plus généraux au plus particuliers.
---> D'après Piaget ce sont les rapports topologiques qui sont d'abord perçus par l'enfant, puis les rap–ports projectifs et enfin les rapports métriques.
III. Des familles de transformations
A. Les homéomorphismes.
La topologie combinatoire étudie les propriétés de l'espace qui sont invariantes par des transformations bijectives et biconti–nues (ces transformations sont appelées des homéomorphismes).
On parle parfois de la géométrie de la pâte à modeler, de la membrane de caoutchouc ou de l'élastique.
Une expérience : Sur une membrane de caoutchouc traçons une courbe fermée. Étirons, déformons sans dé–chi–rer. Que remarque-t-on ?
. Cette transformation "conserve" :
- l'ordre des points de la courbe. - la fermeture des lignes et surfaces
- l'intérieur et l'extérieur. - l'inclusion
- la séparation des points, lignes ou domaines. - la continuité
- le voisinage des points, lignes ou domaines. - l'appartenance
- la tangence - ...
. Par contre les distances ne sont pas conservées, les angles varient, les notions d'orthogonalité et de pa–ral–lélisme sont sans intérêt .....
B. Les projectivités.
On distingue deux familles de projections sur un plan :
- les projections coniques ( appelées aussi centrales ou perspectives)
- les projections cylindriques ( appelées encore parallèles)
o Quelques propriétés invariantes dans les projections coniques:
- l'alignement est conservé ( notion de droite)
- le birapport de 4 points est conservé. ( Et donc aussi les divisions harmoniques)...
o Quelques propriétés invariantes dans les projections cylindriques:
- l'alignement est conservé ( notion de droite)
- le parallélisme est conservé
- les proportions sont conservées ( Soient A , B et C trois points alignés. Les rapports AB/BC ,
AB/AC ... sont conservés) ...
Ces notions sont importantes car :
- notre système de vision fonctionne approximativement comme un système de projection conique.
- l'observation des " ombres au soleil " nous donne une idée des projections cylindriques.
- les travaux sur des représentations planes ( images, photos , plans ) font appel à ces projec–tions.
C. Les affinités.
Elles sont peu étudiées à l'école primaire.
D. Les similitudes.
A l'école primaire c'est selon des critères de similitude que l'on travaille le plus souvent.
E. Les isométries.
Rappelons les noms des isométries du plan:
- les translations de vecteur U - les rotations de centre O et d'angle A
- les symétries par rapport à une droite D - les symétries-translations
- l'identité
Toute isométrie est de l'un de ces types ou peut être exprimées comme composition de certaines d'entre elles.
Lorsque deux figures F et F' se correspondent par une isométrie on parle de figures égales ou superpo–sables.
Faits remarquables :
- il n'y a que 7 types de frises et 17 types de pavages mais une infinité de rosaces.
- certaines isométries change l'orientation.
. Une sous-classification importante selon les éléments de symétrie.
Le monde qui nous entoure est peuplé "d'objets" présentant des "éléments de symétrie".
- symétrie/droite , symétrie/point , axes de répétitions.
Il s'agira pour les maîtres de développer au cours de la scolarité cette connaissance des régularités
c'est à dire de :
a. sensibiliser les enfants à ces propriétés des formes.
b. lui permettre de créer des objets présentant des régularités.
La sensibilisation commence dès l'école maternelle. Les premières images de symétrie que rencon–trent les enfants sont re–latives au corps humain. Dès ses premiers gribouillages par lesquels il tente de re–présenter une personne, les caractéristiques de la symétrie corporelle apparaissent. Il y a dessin natu–rel de symétries dans ses dessins et constructions.
Une série d'activités :
1. Classer des cartons sur lesquels figurent des formes planes présentant 1, 2, 3... axes de symétrie.
2. Donner un matériel qui permettent de construire facilement des figures à 1, 2 , ou 3 axes de symétrie.
- distribuer une famille de gabarits. - collages
- tracés sur géoplan - puzzles à reconstituer
- tampons ...
3. Des figures sont tracées sur du papier non quadrillé, faire tracer les axes de symétrie, indiquer les centres de symétrie.
4. Présenter et faire utiliser diverses méthodes de construction de figures à 1 ou 2 ou plusieurs axes de symétrie.
- tâche d'encre - utilisation du papier calque
- piquage - pliage , découpage
- miroir - tracé libre
- repérage
5. Utilisation de l'ordinateur:
De petits logiciels existent et peuvent servir à créer des figures présentant des éléments de symétrie.
- Frises - Caractor - Grilles - Dessine
V. Etude des formes à l'école.
Quelques objectifs généraux pour l'étude des FORMES :
1. Prise de conscience du concept FORME de la grande variété des exemples.
2.Classification des formes (les placer dans diverses catégories) et dénominations.
3. Structuration des catégories ainsi formées.
4. Construction-reproduction des formes :
. donner peu de contraintes ( créativité …)
. donner de fortes contraintes ( algorithmes de construction…)
La réussite nécessite des savoirs et des savoir-faire des méthodes utilisées et d'autres qualités telles que soin, précision...
Reconnaître une forme c'est la classer dans une certaine catégorie (elle-même repérée par un MOT) . Alors la forme reçoit le nom de la catégorie. Ambiguïtés car il y en général plusieurs catégories d'appartenance (de plus générale et de plus particulières).
Pour réussir la reconnaissance de la forme il faut :
- connaître les attributs essentiels ( et ceux non-essentiels).
- pouvoir vérifier s'ils sont présents ou non.
LES REPERES
I. Repères des Espaces
L'espace habituel (de dimension 3) est muni :
- d'une direction fondamentale : la verticale
- de plans horizontaux
- de "plans inclinés"
Ces éléments sont perçus de façon motrice et visuelle.
- de deux orientations (dextrogyre et androgyre)
Les repères spéciaux:
- les directions ( les points cardinaux N, S, E , O )
- le soleil, la lune ...
-
II. Les repères des objets" (animés et inanimés)
Les objets dans l'espace possèdent ou non des repères :
◊ L'homme
Des plans et axes fondamentaux
- Les trois plans antropomorphiques fondamentaux :
Plans qui vont permettre le repérage du moi par rapport aux objets et des objets par rapport au moi :
. le plan frontal
. le plan fixe sagittal
. le plan mobile horizontal
- Les huit régions déterminées par ces plans
. haute, basse, droite, gauche, devant, derrière, ...
- Les trois directions et des six sens déterminés par les intersections des plans.
◊ Les animaux
Des repères leurs sont attachés.
◊ Autres objets
Certains sont munis de repères de façon permanente ou occasionnelle de manière floue ou non, partielle–ment ou non.
Disons qu'il existe des structurations :
- par projection (translation, rotation, réflexion) de son schéma corporel
- propres liées en général par la forme et/ou l'usage
D'autres objets ne sont pas structurés.
Les repères peuvent être liés à l'objet ou non
o un caillou : le contact indique le bas...
o une bouteille : la forme indique le haut , l' étiquette indique l'avant...
o une chaise : le dossier indique l'arrière,...
o une feuille de papier : ...
o ...
L'apprentissage du vocabulaire spatial est souvent perturbé par l'utilisation de situations mal choisies avec des objets orientés , non orientés , à orientation changeante.
Activité privilégiée qui permet d'aborder de nombreux concepts mathématiques.
Les parcours peuvent être associés à des activités motrices ; ils mettent en oeuvre la notion de codage-déco–dage, de règle, de confi–guration, ... et des notions métriques, topologiques et projectives.
Deux classifications importantes.
- classer selon la dimension de l'espace sous-jacent
- classer selon le critère : parcours libres ou avec contraintes
Activités sur quadrillages divers, labyrinthes...
LE TEMPS
Le "TEMPS" est une composante indispensable et toujours présente dans notre vie, nos actions et nos en–vi–ronnements. Il s'agira d'exploiter les innombrables occasions qui se présentent pour aider les enfants à dé–couvrir cette autre dimension de notre espace qu'est le TEMPS.
I. Placer des "événements-repères" sur l'échelle du TEMPS.
a. La notion d'événement
II. Situer et se situer par rapport à ces "événements-repères".
a. Simultanéité de deux ou plusieurs événements.
b. Position par rapport à un ou deux événements.
c. Découverte et utilisation du "système - standard".
III. Familiarisation avec le concept de durée et sa mesure.
a. Notion de durée.
b. Durée réelle et durée vécue.
c. Mesure de durées.
On arrivera à placer les événements-repères (et à les représenter de manière symbolique sur un axe des temps) en utilisant:
a) les événements qui "marquent les enfants"
- une sortie
- les fêtes religieuses (Noël, Pâques, ...)
- un anniversaire
- fête des Mères ...
-
b) Les événements "courants"
- déroulement de la journée - les saisons
- les jours de la semaine - le matin , le soir...
- le lever et le coucher du soleil - les mois de l'année
c) Les événements "artificiels"
- histoire en images - préparation d'un gâteau
- arrivée d'une course -
. ce sont presque toujours les "pratiques" associées aux événements qui sont mémorisées
- Noël ( arbre de Noel , cadeaux...) -
- Pâques (lièvre de Pâques, oeufs, ....) - La Chandeleur ( crêpes...)
. des attributs permettant la classification des événements
- fréquents, occasionnels, exceptionnels, ponctuels ou non, cycliques....
- passé, présent , futur
. dans certaines situations le TEMPS sera associé à d'autres grandeurs ( VITESSE - ESPACE..)
. les événements cités et les activités qui en résultent ont pour but la compréhension de l'ordre
chronologique, ce n'est pas encore la notion de durée.
. remettre dans l'ordre chronologique une série d'événements est très formateur si l'activité est
associée à la verbalisation.
. le temps s'écoule de façon REGULIERE ( nous ne le percevons pas toujours ainsi ) et dans un
cer–tain SENS ( hélas).
. le PASSE est unique , mais le PRESENT et le FUTUR sont multiples ( choix...) et permettent donc
l'anticipation. ( le jeu est une activité ou le choix et l'anticipation interviennent )
. il est important de garder trace des événements (tenir un Cahier de Vie )
. la durée apparaît comme un intervalle de temps ( la distance entre deux événements , deux
mo–ments.
. la durée vécue nous apparaît différente de la durée réelle.
.Il est important que l'enfant comprenne que :
les événements sont repérés à l'aide:
- d'un système standard : le calendrier
- et d'instruments : montre , .....
les durées sont mesurées à l'aide :
- d'instruments divers:
. montre, chronomètre, sablier, bougie graduée, minuterie...
exprimées par :
- le vocabulaire (mot, verbes, expressions)
. avant , après, pendant, en même temps, simultanément, demain, aujourd'hui, hier....
prochainement, maintenant, plus tard, il y a longtemps, durer, attendre, ...dans le temps,
jadis..
- le temps des verbes utilisés:
. le passé, le présent de l'indicatif , le futur simple...
LE CORPS
La connaissance de l'espace passe par une connaissance, une maîtrise du corps, et par sa structuration.
Le rôle de l'EPS sera d'éduquer la motricité et les conduites motrices qui permettront une meilleure per–cep–tion de l'espace, une meilleure adaptation et entraîneront une amélioration des déplacements.
L'enfant doit prendre conscience :
i. de son corps:
- savoir nommer ses parties, les montrer sur soi-même, sur autrui, ou sur une image un dessin de
personnage ...
ii. des possibilités et impossibilités motrices du corps et de ses parties.
- Découvrir les possibilités et impossibilités motrices des divers éléments corporels et des rela–tions qu'entretiennent ces parties entre elles (observer les dessins d'enfants).
. la tête: elle s'incline,... . la colonne vertébrale: elle se plie,...
. le bassin : il roule,... . le thorax et l'abdomen: ...
. les membres inférieurs:... . les membres supérieurs:...
. .
- Découvrir les possibilités corporelles suivantes :
. courir . sauter . grimper
. ramper . marcher .
. .
iii. des plans et axes fondamentaux
- des trois plans antropomorphiques fondamentaux:
Plans qui vont permettre le repérage du moi par rapport aux objets et des objets par rapport au
moi:
. le plan frontal (fixe)
. le plan fixe sagittal ( fixe)
. le plan mobile horizontal ( mobile)
- des huit régions déterminées par ces plans
. haute, basse, droite, gauche, devant, derrière, , .
- des trois directions et des six sens déterminés par les intersections des plans .
. vers le haut , au-dessus.... . vers le bas , au-dessous
. juste devant . juste derrière
. à ma droite . à ma gauche
. On notera l'importance et l'antériorité de la prise de conscience de l'axe vertical. La direction haut->bas est privilégiée car per–çue de façon motrice et visuelle très précocement (chutes de l'enfant ou des objets ..)
. Les notions de haut-bas et droite-gauche apparaissent comme des oppositions. L'apparition d'une prédo–mi–nance de la main favo–rise le renforcement d'un côté du corps (soit droit soit gauche).
. On considère qu'à partir de 5 ans un enfant localise sur soi et nomme correctement les 20 parties sui–vantes de son corps :
- cou - dents - nez - pied - menton - joue - épaule
- yeux - ge–nou - front - cheveux - dos - talon - bouche - oreilles - pouce - ongles - ventre - main
LA FONCTION SYMBOLIQUE
La fonction symbolique se développe chez l'enfant à partir de deux ans environ. Elle permet d'évoquer le si–gnifié (objet, action, sentiment, concept..) à partir d'un signifiant ( mot, geste, image, dessin....) .
Elle naît de la nécessité de communiquer,mais aussi de garder trace d'actions.
La fonction sémiotique permet l'abstraction, l'évocation d'objets ou d'actions que le sujet ne peut con–tem–pler. Le symbolisme se construit à partir de jeux, elle se développe par imitation et grâce au lan–gage.Toute notion nouvelle est intégrée dans les schèmes antérieurs (phénomène d'assimilation) mais en même temps il faut accommoder ses schèmes (phénomène d'accommodation).
La société nous fournit de nombreux exemples où les objets, les actions, les relations sont représentés par des symboles ou des signes.
L'objet, l'action, la relation que l'on veut désigner prend le nom de signifié. Le symbole ou le signe permet–tant de désigner le si–gnifié s'appelle le signifiant.
On distingue deux sortes de signifiants: les symboles et les signes. Le symbole est un signifiant mo–tivé, c'est à dire témoignant d'une certaine ressemblance avec le signifié. L'observateur peut découvrir seul le signifié à travers le signifiant. Le signe est un si–gnifiant arbitraire lié à son signifié par une con–vention so–ciale. L'observateur ne peut découvrir le signifié à partir du signe. Il est nécessaire de connaître la con–ven–tion. Souvent le signifiant résulte de la combinaison d'un signe et d'un symbole. Les signifiants sont so–nores et/ou visuels. Signifiants sonores : langage parlé, musique, cloche , bruit....
Signifiant visuel : langage écrit, signaux lumineux, gestes, images, pictogrammes, dessins...
Un signifié peut être désigné par un ou plusieurs signifiants différents (synonymes).
Ce qui est non satisfaisant c'est d'employer le même signifiant pour deux signifiés différents (homonymes).
C'est en employant des signes qu'on communique la pensée mathématique. La symbolisation est un pro–blème important et source de difficultés qu'il ne faut pas sous estimer.
LE NOMBRE ENTIER
I. Sa construction sur le plan psychologique.
L'observation des enfants de 2 à 7 ans nous fait comprendre qu'il y a plusieurs niveaux de connaissance du nombre.
A. un niveau de connaissance verbale :
L'enfant connaît (apprend par coeur) certains noms de nombres, mais l'ordre sur les nombres est mal assuré , la liste des mots connus limitée. S'il compte sur les doigts, le mot est attaché à un doigt particulier, il a l'impression qu'il lui faudrait une in–finité de mots différents pour savoir compter.
Le milieu familial et l'école assurent un enrichissement de la comptine habituelle, mais très souvent l'enfant n'arrive pas à compter oralement à partir d'un nombre autre que "un".
B. Un niveau de connaissance visuelle :
Certaines petites collections sont reconnues rapidement après dénombrement unité par unité ou globa–lement. La limite de reconnaissance globale est de 4 ou 5 objets ou un peu plus si les objets sont bien disposés ou si l'on utilise un matériel particulier . (dominos ... réglettes Cuisenaire..)
C. Un niveau de connaissance opératoire :
i. Premier sous-niveau :
L'enfant commence à dénombrer une collection en se servant de la comptine. Il associe (par geste) un mot (un numéro) à un objet, mais il se trompe encore. Il n'est pas rare qu'à la question : combien d'objets y a-t-il ? l'enfant réponde correctement dans un premier temps mais éprouve le besoin de recompter à la suite d'une réorganisation des objets. La nature des objets, leur dis–position spatiale, la "taille" de la collec–tion influen–cent sa réponse.
La comptine apparaît comme une suite ordonnée et finie de mots sans grands liens les uns avec les autres. De nombreuses mal–adresses subsistent : on oublie de compter certains objets et d'autres sont comptés plusieurs fois.
ii. Deuxième sous-niveau :
L'enfant devient capable d'utiliser très bien la comptine qu'il con–naît. Il arrive à comparer le nombre d'éléments de 2 collections grâce à l'appariement (établissement d'une bijection ou correspondance terme à terme) est dire s'il y a "autant , plus ou moins " d'éléments dans l'une et l'autre collection.
Cette correspondance peut être spontanée, provoquée ou intelligente dans la mesure où l'enfant à compris qu'il dispose d'un moyen puissant pour comparer le nombre d'éléments de deux collections.
iii. Troisième sous-niveau :
L'enfant à dépassé le stade des apparences, il n'est plus prisonnier de ses perceptions. Il y a conservation du nombre et des ensembles. La correspondance terme à terme est bien maîtrisée et durable. Il sait distin–guer la partie du tout , a compris que le tout est un as–semblage de par–ties que l'on peut distribuer comme on veut.
Il sait sérier des objets. Il est capable de revenir en arrière par la pensée et par l'action.
II. Sa construction sur le plan mathématique.
A. Construction ensembliste ("cardinale"):
On définit sur la "classe de tous les ensembles" une relation d’équivalence :
Deux ensembles A et B sont équipotents (ont même cardinal, ou même nombre d'éléments) s'il existe une bijection de A sur B.
Le nombre entier apparaît alors comme classe d'équivalence.
B. Construction axiomatique ("ordinale"):
On définit une suite d'ensemble à partir de l'ensemble vide. Cette suite forme un ensemble noté N qui vérifie les axiomes de PEANO :
. 0 est entier naturel.
. Tout entier naturel a un successeur.
. Deux entiers naturel ayant le même successeur sont égaux.
. 0 n'est le successeur d'aucun entier naturel.
. Si une partie P de N contient 0 et si le successeur de tout élément de P appartient à P , alors P égal N . (c'est l'axiome de récurrence)
Voici la suite des premiers "ordinauxe :
ø ; { ø } ; { ø , { ø } }; { ø , { ø } } ; { ø , { ø , { ø } } } .....
Le successeur de l'ensemble X sera l'ensemble X U { X } noté aussi X+
III. Sa construction sur le plan pédagogique
L'étude des I.O. de 1945,1970,1977 et 1985 montre que les choix pédagogiques pour la construc–tion du nombre sont inspirés des deux constructions théoriques précédentes sans que l'une ou l'autre de ces cons–tructions ne se soit définitivement impo–sée.
A. D'après les I.O de 1945 :
On apprend aux élèves,la suite des nombres (nom et écriture) en base dix ,et l'on dénombre les col–lections d'objets par l'intermédiaire de cette comptine. Les nombres sont étudiés un à un dans l'ordre de leur apparition dans cette comptine. Chaque nombre apparaît comme étant une sorte de qualité, concréti–sée par une (parfois plusieurs) configuration(s) particulière(s) et ayant une écriture et un nom unique.
"Pour avoir véritablement la notion de nombre, il faut pouvoir le reconnaître sous ses aspects divers :connaître son nom, sa figure, sa configuratione .
On traite simultanément les problèmes d'existence, d'ordre et d'écriture, l'aspect ordinal du nombre est privilégié, l'aspect cardinal ignoré. On ne tient pas compte des difficultés mises en évidence par la psy–cho-génétique. La connaissance du nombre est trop axée sur la perception et la mémorisation, on oublie que le nombre n'est pas de l'ordre du voir mais du concevoir.
B. D'après les I.O de 1970.
L'accent est maintenant mis sur l'aspect cardinal du nombre. On fait classer un certain nombre d'ensembles finis suivant la relation d'équipotence. Les nombres apparaissent alors comme des classes d'équivalence, ils ne sont pas une propriété d'objets mais de collections d'objets.
Donner un nom à ces classes peut se faire de nombreuses manières, en particulier à l'aide de sys–tèmes de numération à base b. Les classes d'équivalence sont ensuite ordonnées ( introduction de la rela–tion d'ordre ≤ ). Le nombre est introduit tardivement au CP.
C. D'après les I.O de 1977 et 1985.
La présentation du nombre préconisée par le programme de 1970 est maintenue , mais l'aspect ordi–nal qui avait été un peu négligé est remis en valeur. L'enrichissement et la maîtrise de la comptine reste im–portant (cela va dans le sens du développe–ment des acquis), mais il ne s'agit pas pour autant d'évacuer l'aspect cardinal.
On insiste sur la découverte des systèmes de numération de position, tout en rappelant que la pré–sen–tation des bases infé–rieures à dix n'est qu'un moyen pédagogique destiné à mieux faire comprendre et assimi–ler la base dix. On conseille aux maîtres d'éviter les excès dans l'étude des "bases".
On abordera “aussitôt que possible le nombre et l'acquisition sera relativement lente jusqu'à vingt" . La correspondance terme à terme fournit un moyen pour comparer les collections. Il faut se sou–venir que les facteurs d'évolution dans l'assimilation du nombre sont (entre autres) :
- l'action personnelle combinée à la réflexion et la perception.
- le développement de la mémoire
- l'âge car un niveau de maturation est nécessaire.....
IV. Des prés requis :
- Permanence de l'objet :
. l'objet que l'on cache est toujours là
- Constance de la grandeur :
. l'objet reste de même taille si on l'éloigne
- Conservation des ensembles :
. existence d'un ensemble non liée à la proximité spatiale des éléments
- Existence d'un temps homogène :
. temps non lié à la nature des événements
- Constance de la forme :
. l'objet reste le même quel que soit le point de vue
- Conservation des quantités discontinues :
.
- Connaissance et conservation des correspondances "terme à terme" :
.
- Compréhension de la notion d'inclusion :
.
- Capacité de composition de relations :
.
- Capacité de symbolisation :
.
- Connaissance des classifications :
.
- Connaissance des sériations :
- Perception des relations de "cause à effet" :
.
V. A propos de la comptine.
Une comptine standard importante : un, deux, trois,....
Il faut examiner de près cette comptine numérique et surtout les modalités qui permettront, à partir d'un statut verbal de la faire évoluer vers un signifiant numérique. Ceci suppose la maîtrise du principe d'abs–traction (ne pas tenir compte de la nature des ob–jets à dénombrer) du principe de cardinalité : le der–nier mot prononcé désigne le cardinal de la collection et celui-ci ne dépend pas de l'ordre dans lequel les objets sont dénombrés
L'enfant apprend à compter très tôt dans son milieu familial. C'est un fait dont il faut tenir compte.
Compter, ce n'est évidemment pas une preuve de la maîtrise du nombre.
Compter c'est associer un mot à une information (à caractère numérique associée à un ensemble) mot qui dé–signe un cardinal ou un ordinal.
Compter c'est connaître une suite ordonnée appliquée bijectivement aux doigts et aux objets et qui associée à un pointage de l'in–dex se maîtrisera plus facilement.
VI. La reconnaissance globale des petites collections
la perception globale instantanée ( encore appelée "subitzing" ) du cardinal de petites collections semble dé–pendre du niveau d'âge et de la constellation utilisée.
la capacité de reconnaître de petites collections semble dépendre du niveau d'âge et de former des collections équiva–lentes semble dépendre de l'âge comme indiqué dans le tableau ci-contre:
Les tout-petits: 1 ≤ n ≤ 3
Les petits : 1 ≤ n ≤ 4
Les moyens : 1 ≤ n ≤ 7
Les grands : 1 ≤ n ≤ 17
Longueur, aire, masse, capacité, température sont les principales autres grandeurs que l'on tentera d'aborder à l'école maternelle.
LES CONCEPTS
I. Généralités
Quand on apprend un concept, on apprend à reconnaître et à distinguer les "attributs" qui le spécifient.
Un attribut est ce qui permet de distinguer un objet d'un autre objet, une idée d'une autre idée....
Si l'on veut identifier un objet (ie déterminer son appartenance à une classe) l'attribut doit se référer aux caractéristiques qui per–mettent de le classer dans une catégorie fondamentale ; ce sont les attributs es–sen–tiels. D'autres qualités connues ou inconnues, pour–ront servir à les décrire et non pas à les définir, ce sont les attributs non essentiels. Chaque attribut peut avoir des "valeurs" diffé–rentes.
Pour pouvoir désigner cette combinaison d'attributs on la nomme par un mot qui est un symbole arbitraire -son ETIQUETTE -. Cette ETIQUETTE nous permet de regrouper tous les exemples qui possèdent la même combi–naison d'attributs dans la même caté–gorie,quelles que soient les différences par ailleurs. Il est im–portant de comprendre que l'étiquette n'a pas à elle seule de l'impor–tance, ce qui est essentiel c'est de sa–voir pourquoi on appelle un objet, une idée par ce nom et comment il est relié à d'autres concepts.
Un concept c'est donc un MOT ( une dénomination,une étiquette) non pas isolé mais qui désigne une liste d'attributs essentiels. Ce mot est susceptible d'être appliqué à des EXEMPLES.
-On perçoit les analogies entre la notion de concept et les notions d'ensemble et de relation d'équivalence en mathématiques.
Le terme "notion" est souvent pris comme synonyme d'idée, de pensée abstraite et renvoie à l'acte par le–quel l'esprit conçoit les "caractères essentiels" d'un objet,d'une idée, d'un principe ...
Le cadre notionnel d'une théorie ce sont les concepts ou notions de base, dont le réseau constitue le cadre théorique. Attention, il arrive que la même étiquette appartienne à des réseaux conceptuels disjoints.
II. Classifications des concepts
Une double classification des concepts selon J. BRUNER
Elle résulte
- d'une part du type de relations existant entre les attributs essentiels.
On distinguera les concepts :
a. conjonctifs
b. disjonctifs
c. relationnels
- d'autre part on distinguera les concepts selon
1. le niveau de complexité
2. le niveau d'abstraction
3. le niveau de validité
a. Les concepts conjonctifs.
Ils sont définis par un ensemble d'attributs qui sont tous présents dans chaque exemple donc reliés par les connecteurs "et".
Exemple: ...
b. Les concepts disjonctifs.
Ils sont définis par un ensemble d'attributs qui ne sont pas tous nécessairement présents donc reliés par les connecteurs "ou".
Exemple : ...
c. Les concepts relationnels .
Ces concepts ne peuvent se définir que par rapport à d'autres attributs "opposés".
Exemples :
. grand - petit
. haut - bas
. rouge - non rouge
1. Le niveau de complexité dépend :
- du nombre d'attributs essentiels qui le caractérise. Plus il y a d'attributs essentiels plus il est
réputé complexe.
- et de la nature des attributs à savoir observables ou non.
2. Le niveau d'abstraction ou de généralité.
3. Le niveau de validité.
III. Les concepts fondamentaux
L'on peut imaginer qu'il existe des "concepts fondamentaux" communs à diverses disciplines et penser que le but de l'éducation de base devrait être essentiellement d'agir au niveau des démarches et concepts communs.
Existe-t-il de tels concepts ?
Il est bien sûr difficile de répondre à cette question, de donner la liste, néanmoins il semble que l'on puisse les regrouper autour d'un certain nombre de valeurs sémantiques primitives élaborées à partir des sens.
Tout individu qui vit qui voit une situation reçoit d'elle une multitude de sensations. De cette foule de sen–sa–tions, les centres sous-corticaux opèrent une sélection. .Seules celles qui franchissent le seuil de la cons–cience deviennent des perceptions, ce sont celles qui répondent aux besoins et aux intérêts des sujets.
Quelles sont ces valeurs sémantiques primitives ?
Ce sont les concepts de :
. grandeur . vitesse . direction . situation
. orientation . relation . intensité
Ces notions sont découvertes, développées,affinées grâce aux activités de perception d'où le rôle capital de l'EPS qui développe les perceptions motrices et visuelles.
Comment ces concepts se forment-ils?
Découverte des concepts grâce aux oppositions. Puis combinaisons d'oppositions.
En mathématiques, cela revient à présenter une propriété et sa négation. Puis à relier des propriétés grâce aux connecteurs (et,ou, non).
Une perception est spontanément privilégiée lorsqu'elle se trouve en opposition avec une perception de même ordre et de sens contraire qui, lui succède lui coexiste ou lui précède.
- (Par exemple la notion de grandeur ne peut naître que de l'opposition grand-petit)
Pour le maître il s'agira donc de faire vivre des situations (motrices) successives similaires dans les–quelles un (ou à la rigueur deux) éléments ont été changés. On suscitera une analyse perceptive puis un passage à la modélisation, à l'abstraction.
Quelques oppositions absolues
1. Matière et néant. 2. Masse et rien. 3. Plein et vide.
4. Bruit et silence. 5. Lumière et obscurité.
Quelques oppositions relatives
Celles liées à l'intensité
a1 . fort et faible a2 . dur et mou a3 . lourd et léger
a4 . Beaucoup et peu a5 . Clair et sombre a6 . grave et aigu
a7 . Chaud et froid a8 . rugueux et lisse a9 . sec et mouillé
a10. bon et mauvais a11. a12.
Liées à la grandeur :
b1 . grand et petit b2 . long et court b3 . épais et mince
b4 . gros et maigre b5 .
Liées à la vitesse :
c1 . vite et lent c2 .
Liées à la situation, à l'orientation:
d1 . loin et près d2 . dedans et dehors d3 . entre et "non entre"
d4 . en haut et en bas d5 . devant et derrière d6 . à droite de et à gauche de
d7 . vertical ou horizontal d8 . sur et "sous" d9 . droite te gauche
d10. à côté de de et "non à côté de " d11. Sens dextrogyre et génogyre Liées au temps :
e1 . début et fin e2 . avant et après e3 . simultanément ou non
e4.
Liées à la logique :
f1. Appartenance ou non appartenance f2 . oui - non f3 . vrai - faux
f4 .
Liées à l'affectif :
g1 . gai et triste g2 . beau et vilain g3 . calme et agitation
g4 . espoir et désespoir g5 . donner et recevoir g6 . gentillesse et "non -gentillesse"
g7 . Joie et colère g8 . douleur ou non-douleur g9 .
QUELQUES CONCEPTS MATHEMATIQUES
I. Le concept de PROPRIETE.
Il y a lieu de distinguer les propriétés absolues et les propriétés relatives.
Les objets tant réels que mathématiques sont caractérisés par un certain nombre de propriétés. Il y a lieu de connaître celles qui sont essentielles.
II. Le concept d'ENSEMBLE.
Rappels :
a. Un ENSEMBLE peut être défini de diverses façons :
1. En extension
C’est-à-dire en se donnant la liste exhaustive des éléments le constituant
Par exemple : { LUNDI , SAMEDI , DIMANCHE , MARDI , MERCREDI , JEUDI , VENDREDI }
2. En compréhension
C’est-à-dire par une propriété commune exprimée par une phrase
( Un prédicat de poids un, deux, ...).
Par exemple : { les jours de la semaine} , { les nombres entiers premiers } , { les triangles } , …
b. Un SOUS-ENSEMBLE est un ensemble particulier, il est considéré comme inclus dans un ensemble
appelé UNIVERS qu'il est nécessaire de connaître.
Ce sous-ensemble peut être défini de différentes manières.
1. Par un tableau d'appartenance :
En face des divers éléments, on écrit (V ou F ) , ( 0 ou 1) , ( une croix X ou pas de croix)
2. Par un diagramme ( une patate):
On entoure par une ligne simple fermée les éléments appartenant au sous-ensemble.
Exercice difficile si les éléments du sous-ensemble sont représentés de façon dispersée sur une
feuille.
3. Par un marquage:
Les éléments du sous-ensemble sont marqués ( coloriage , soulignage, cochage...). L'on peut aussi
barrer les éléments n'appartenant pas au sous-ensemble.
4. Par un regroupement ( séparation spatiale):
On peut utiliser cette technique si l'on travaille avec des éléments manipulables.
5. Par une application f :
L'image d'un élément qui appartient au sous-ensemble est 1. L'image d'un élément qui n'appartient pas
au sous-ensemble est O . Remarquez que f -1(x) défini aussi un ensemble
6. Par une propriété commune :
Exemple : { les blocs logiques rouges}
7. Par la liste des éléments constituant le sous-ensemble :
Exemple : Pierre et Paul deux garçons de la classe de 6 ème 1.
Remarques :
- Il ne faut pas sous-estimer les problèmes liés aux désignations, représentations des éléments et de
l'ensemble lui-même .
- La définition d'un ensemble en compréhension suppose que l'on sache ce qu'est un prédicat de poids
un, voire deux ou trois.
- Théoriquement les éléments d'un ensemble doivent êtres distincts et donc distinguables. Ce qui vous
permettra d'éliminer comme incorrects 95 % des exercices présentés dans les livres.
- Le mot COLLECTION est souvent utilisé à la place du mot ENSEMBLE.
-
III. Le concept de RELATION.
On entend par relation un type particulier d'énoncé qui s'exprime en général par une forme verbale affirmative avec un verbe d'état ou d'action. Elle peut lier un , deux , ou davantage "d'objets", objets ap–par–tenant à 1 voire plusieurs ensembles .
Un exemple de relation unaire ( ou propriété simple):
Voici une collection E de blocs logiques. On se donne le prédicat " x est ROUGEe. Pour chacun d'eux on obtient une proposition en remplaçant x par un élément de l'ensemble. Certaines de ces proposi–tions sont vraies, d'autres fausses. Les éléments (objets) de la collection pour lesquels la proposition est vraie for–ment un sous-ensemble A (qui peut parfois être vide !) . On no–tera A = { x C E p(x) } . Vous savez que les éléments (objets) de la collection pour lesquels la proposition est fausse forment aussi un sous-ensemble noté A et défini par A = { x C E ¬ p(x) }
IV. Les structures de DONNEES.
Les files
Les suites.
Les tableaux
Les arbres
V. Les ALGORITHMES.
Rappel :
Trouver un algorithme, c'est analyser la situation, indiquer les tâches élémentaires et leurs enchaîne–ments.
Deux objectifs :
- Trouver un algorithme
- Appliquer un algorithme
Les deux types d'algorithmes
--> Les algorithmes simples (ou répétitifs)
--> Les algorithmes complexes (ou récursifs)
VI. La LOGIQUE.
1. Les relations de cause à effet
2. Les connecteurs NON , ET , OU
CHAPITRE 3. Un Objectif prioritaire.
I. Analyser.
Développer chez nos élèves
la capacité d'analyse des "configurations".
Des exemples:
- un mot est constitué de caractères appelés lettres .
- une phrase est constituée d'entités appelées mots .
- un nombre (donné sous la représentation décimale canonique) est constitué de signes appelés chiffres .
- un triangle est constitué d 'objets géométriques appelés segments .
.... et l'on pourrait multiplier les exemples.
Nous nous intéresserons plus particulièrement à l'analyse de configurations d'objets géométriques.
Rappelons qu' Analyser pourrait signifier :
- percevoir des parties.
- percevoir des ressemblances et des différences.
- percevoir des relations :
◊ appartenance
◊ inclusion
◊ union
◊ séparation
◊ positions
◊ intersections
◊ orientations
◊ équivalences
◊ régularités
◊ ....
CHAPITRE 4. Quelques familles d'activités
I. Activités ludiques
Un plaidoyer pour le jeu à l'école.
L'importance du jeu pour l'enfant ne saurait être mise en doute.
Certes il ne s'agit pas de fonder la pédagogie sur l'amusement et ouvrir la porte à la facilité, à la démago–gie, à la médiocrité et ris–quer ainsi de ne pas favoriser la structuration du savoir et son développement. Le rôle de l'éducateur est ici fondamental ; c'est à lui de choisir, de penser, de fournir situations et maté–riels conve–nables afin qu'en jouant l'écolier assimile des réalités intellectuelles qui, sans les conduites lu–diques appro–priées seraient demeurées extérieures à son intelligence.
Un dossier à réaliser :
Sélectionner, collecter, construire des matériels. Penser, expérimenter des situations destinées à fa–vori–ser le développement intel–lectuel des enfants dans sa composante mathématique principalement.
Des jeux "logiquese
. blocs logiques
. matériels pour classements et rangements
. jeux d'associations
.
Des jeux de "mémoire" .
. mémory
. jeux d'observation
.
Des jeux "spatiaux"
. puzzles et pavages
. jeux de formes
. jeux sur quadrillage et damiers
. pliages et tissages
.
Des jeux "divers" .
( Voir le livre de Mme WINNINGER )
.
.
.
Des matériels "divers"
. construction de calendriers
. construction de mobiles
. construction de maquettes
.
II. Activités combinatoires et agencements
I.Pourquoi faut-il accorder de l'importance aux activités combinatoires ?
Sur le plan intellectuel et le plan conceptuel, elles :
. développent l'esprit logique.
. facilitent le passage du concret à l'abstrait.
. stimulent l'imagination et la créativité.
. renforcent la mémoire visuelle.
. conduisent à la découverte et à l'organisation de l'espace grâce:
- à un affinement des perceptions visuelles et tactiles
- une découverte de nombreuses relations spatiales.
. permettent une approche des notions:
- d'équivalence des formes - de mesure - de transformations géométriques
. donnent naissance à des problèmes combinatoires.
. servent de support à des démonstrations mais peuvent aussi , souligner le danger "d'une
démonstration par la manipulation" ,
faire sentir le besoin d'une "vraie démonstration".
. développent l'esprit critique...
Sur la plan pédagogique elles:
. sont basées sur l'opérativité de l'élève.
. font office de situations motivantes pour l'introduction ou le renforcement de certains concepts.
. nécessitent souvent un travail par groupes.
. permettent de mettre en oeuvre une pédagogie différenciée, car il est facile de varier les
difficul–tés des situations-problèmes.
. peuvent être auto-correctives...
A. Que peut-on agencer ou réagencer ?
a. Des formes.
- des lignes (familles particulières, quadrillages.....)
- des surfaces (pavages, puzzles, frises, rosaces....)
- des solides (empilements, jeux de construction, puzzles.....)
b. Des "objets" .
- baguettes, réglettes , ficelles...
- dominos divers .
- lettres , mots (anagrammes , mots croisés...)
- images (mémorys, jeu des familles...)
- cartes
- dés ...
B. Ce que disent les I.O à propos des agencements.
a. D'après les I.O de 1970 .
Développement de la perception :
En maternelle et au cycle préparatoire :
"Au cours de ses jeux, de ses activités spontanées l'enfant est naturellement appelé à observer le monde qui l'entoure....par des jeux libres d'assemblage, de juxtaposition, de mélange d'éléments naturels ou éla–borés , l'enfant doit devenir apte à découvrir dans le contact sensoriel avec la matière et le matériau , la multipli–cité de leurs aspects, les effets offerts par leurs rapports de couleur et de forme, la possibilité d'en modifier l'état immédiat en vue d'une organisation créatrice personnelle..."
"... l'enfant doit pouvoir ... aligner ou étaler selon certaines formes des objets..."
Reconnaître des formes et des figures simples :
- pavages, mosaïques, puzzles.
Organiser:
- successions régulières,frises...
- jeux de construction, d'emboîtement.
"... ces activités contribuent cependant toutes à la formation de la pensée logique et préparent de façon intui–tive la prise de conscience de propriétés géométriques qui seront dégagées par la suite..."
Activités d'agencement ou d'assemblage (à plat ou en trois dimensions)
- collages, emboîtements, encastrements.
- agencements variés,...mosaïques.
- divers jeux de construction (des blocs de bois aux jeux du type MECCANO).
-
b. D'après les I.O de 1985 et 1986 .
".. les activités scientifiques et techniques permettent à l'enfant d'explorer, de découvrir et de fabri–quer. Il observe, utilise des ma–tières et des matériaux présents dans le coin de bricolage, choisit des techniques (collage, pliage, assemblage, clouage, montage et démontage,..). Il fabrique ainsi des objets nouveaux..."
"Ce faisant, l'enfant déploie, découvre et organise les relations logiques et mathématiques qui fondent la construction des objets, le repérage de leurs propriétés, et l'établissement des classifications".
"...rosaces, frises, pavages, mosaïques, puzzles."
C. Les puzzles dans le plan et l'espace.
Les divers types de puzzles du plan.
Pour certains, c'est surtout la forme des pièces qui joue le rôle principal.
Pour d'autres, c'est l'idée qui domine.
Parfois on dispose de modèles.
a. La réalisation avec planche-modèle peut se faire de diverses façons :
1. On place les pièces du jeu directement sur le modèle.
(approche analytique)
2. On reproduit la configuration à côté de la planche.
(approche synthétique)
3. On réalise le modèle dans une autre taille ou avec des variantes ou de plusieurs façons.
(approche globalisante)
b. La réalisation sans modèle peut se faire:
1. Sans consignes.
(approche créatrice)
2. Avec consignes orales avec nécessité de prévoir les dimensions ou la forme du modèle.
(approche anticipatrice)
Trois jeux d'assemblages
a. Un puzzle très connu
le TANGRAM
Voir Grand N IREM de Grenoble n° 18
b. Les carrés bicolores
On assemble 4 carrés identiques au modèle présenté ci-dessous, pour former un nouveau carré. Faire l'inventaire des figures obte–nues, étant entendu que l'on considérera comme équivalentes deux figures qui se déduisent l'une de l'autre par rotation ou symé–trie.
c. Les polyminos
Rechercher tous les assemblages de 3,4,5 carrés (les polyminos). Annexe n°1
I.O. de l'école maternelle
Ce que disent les I.O. de 1977
o L'enfant doit être capable :
... d'employer les termes relatifs aux relations de temps et d'espace...
o ... familiariser l'enfant avec l'utilisation de quelques instruments ( par ex: la règle et l'équerre) au
cours des activités manuelles ne saurait être néfaste en soi : mesurer, évaluer , tracer ...
o L'enfant doit pouvoir :
... manipuler , grouper, regrouper des objets après les avoir séparés.
... vider, remplir des vases ou des récipients divers, transvaser des liquides.
o L'organisation du milieu doit permettre aux enfants:
... de participer à des parcours déterminés par des objets fixés au sol.
... de poursuivre des itinéraires jalonnés ou non.
o L'enfant doit successivement devenir apte à :
- déchirer , déchiqueter du papier.
- découper du papier , du carton.
- coller.
- ajuster des pièces initialement séparées.
o Un autre objectif est celui de la découverte par l'enfant à travers ses propres réalisations en sur–face ou en volume des rythmes agréables à l’œil, des couleurs séduisantes, des formes les plus belles pour lui...
o par des jeux libres d'assemblages, de juxtapositions , de mélange d'éléments naturels ou élabo–rés, l'enfant doit devenir apte à découvrir dans le contact sensoriel avec la matière et le matériau la mul–tiplicité de leurs aspects, les effets offerts par leurs rapports de couleur et de forme...
o Traduire par le dessin, la peinture, le modelage et les constructions en volume les images qu'il porte en lui.
o Classer des images séquentielles de gauche à droite en les ordonnant selon le sens du récit.
o L' enfant doit pouvoir
- manipuler des objets
- reconnaître leurs propriétés
- les déplacer, les regrouper ou les ranger
o L'important est de former les esprits à la réflexion, à la recherche. La créativité à la fois effet et source de l'intelligence divergente trouve également sa place en mathématiques où certains croient de–voir cultiver exclusivement l'intelligence conver–gente.
Ce que disent les I.O. de 1985
o Il établit des sériations, c'est à dire ordonne des collections en fonctions de propriétés.
o L'enfant découvre et construit le nombre. Il apprend et récite la comptine numérique.
o Il compare des collections terme à terme.
o Il découvre et construit des relations spatiales (voir I.O p 61)
Ce que disaient les programmes de 1887
Les programmes de 1887 qui ont été modifiés en partie par des textes officiels de 1905 1908 et 1922
Petite section :
Groupements très variés d'objets semblables : 2 , 3, 4 , 5 jusqu'à 10, et compte de ces objets ( sacs individuels de cailloux, bâtonnets, coquillages ...)
Grande section :
Groupements d'objets: 20, 30, 40 , jusqu'à 50 ( sacs individuels)
Demi, moitié, tiers, quart .
Petits exercices de calcul mental : additions, soustractions, multiplications, divisions.
Représentation des nombres, de l'unité jusqu'à 50. Petits exercices écrits de calcul avec dessins
correspondants. Exercices et jeux avec le mètre, le franc, le litre, les poids (balance, kilogramme, demi-kilogramme) .
Ce que disent les I.O. de 1995
Classifications, sériations, dénombrement, mesurage, reconnaissance des formes et des relations spatiales.
Tous ces instruments du travail intellectuel qui deviendront plus tard des opérations de l'activité mathématique son t particulièrement utiles pour décrire la réalité et pour comprendre les phénomènes qui y surviennent.
Classifications et sériations
Progressivement l'enfant découvre et organise les relations logiques en travaillant sur des collections d'objets. Pour cela, il peut procéder à:
• des classements d'objets en fonction de l'une de leurs qualités
• des rangements d'objets, en particulier grâce à des critères quantitatifs( plus grand, plus gros, plus large, ...)
• des comparaisons de collections, conduisant éventuellement à compléter certaines d'entre elles;
• des désignations et des symbolisations
L'enfant peut utilement travailler sur les sériations et les rythmes ( listes, récits, bandes dessinées, frises...) et pratiquer des jeux à règles.
Approche du nombre
Pour le jeune enfant, la quantification du monde qui l'entoure n'est pas d'emblée numérique, les quantités à estimer ou à produire peuvent dépasser ses possibilités de dénombrement.
Progressivement, il apprend à construire un certain nombre de procédures et d'outils pour dénombrer les collections d'objets:
• estimation relative et globale de petites collections par une perception instantanée.
• dénombrement de petites collections par une perception instantanée;
• comparaison de collections à des collections naturelles ( doigts de la main) ou à des collections repères (nombre de places autour de la table, ...)
• fixation et extension de comptine parlée;
• dénombrement en utilisant la comptine.
A travers la résolution de petits problèmes additifs ou soustractifs et de situations de distribution d'objets, l'enfant découvre les fonctions du nombre, en particulier comme représentation de la quantité. Le nombre permet aussi par son aspect ordinal, de décrire des hiérarchies et des rangements. Les activités porteront sur :
• la hiérarchisation de séries en utilisant la comptine numérique;
• la comparaison de certaines dimensions des objets en utilisant un étalon.
Reconnaissance des formes
Les formes sont des propriétés des objets ou des espaces qui doivent être reconnues, construites, tracées. La multiplication des expériences diverses, dans des espaces proches ou lointains, avec des objets petits ou grands, est nécessaire à l'enrichissement des observations qui préparent à la géométrie. Les activités peuvent s'organiser autour:
• de la découverte de formes fermées ou ouvertes, des notions d'intérieur et d'extérieur;
• de la différenciation et de la classification de formes, régulières ou irrégulières, mettant en jeu des dénombrements ( nombre de sommets, de côtés, de faces...);
• de la désignation de formes.
Repérages dans l'espace
Se repérer dans l'espace, se déplacer selon des consignes strictes, manipuler les indicateurs spatiaux du langage, sont des activités qui s'ordonnent tout au long du cursus de l'école maternelle. L'école maternelle doit permettre à l'enfant de donner du sens à ce repérage en passant de son point de vue à celui de ses camarades au travers d'activités nombreuses et diverses, jouant sur les trajets et parcours, réels ou représentés, et incluant leur description verbale. Progressivement, il construira :
• une organisation de l'espace proche et lointain par rapport à celui qui parle( près de moi, à côté de moi, ici, ... s'opposant à loin de moi, là-bas...);
• une organisation des différentes dimensions de l'espace à partir de celui qui parle( dessus, dessous, au-dessous, à gauche, à droite,...);
• une organisation de l'espace par rapport à des objets ou à des repères extérieurs( près de la porte, au fond du couloir...)
On utilisera les mêmes indicateurs, ou d'autres, pour repérer les objets dans un espace réel ou représenté.
Repérage des événements dans le temps
Les repères temporels introduisent aussi bien à la description des phénomènes physiques qu'à l'histoire des hommes. On procédera à leur mise en place grâce à :
• une prise de conscience de l'opposition passé/présent par rapport au moment de la prise de parole;
• une prise de conscience du futur comme attente, projet, souhait...
• une exploration et une fixation du lexique de l'énonciation temporelle ( maintenant, avant, après, hier, demain...);
• une structuration du temps à partir des activités revenant régulièrement;
• une prise de conscience des grands rythmes naturels (nuits/jour, saisons, années, ...) et leur utilisation comme repères chronologiques;
• une mise en place de repères chronologiques communs à la classe, à l'école;
• une fixation et une utilisation du lexique des repères temporels ( matin, après-midi, soir, nuit, ...) et des comptines temporelles ( heures, jours de la semaine, mois de l'année, ...);
• une mise en ordre des événements passés par l'usage des temps des verbes;
• une appréciation, une comparaison des durées;
• une première approche de la simultanéité.
Dessiner, écrire, dénombrer, mesurer, décrire l'espace, se repérer dans l'espace et le temps constituent des instruments puissants de la connaissance. Permettre à l'enfant de les construire dès l'école maternelle est un gage de réussite ultérieure dans sa scolarité.
BIBLIOGRAPHIE
1. Au fil de l'an . Y.SCHEUBEL (CDDP COLMAR)
2. Eveillez l'intelligence de votre enfant. E.OTT (CASTERMANN)
3. Les premiers pas en mathématiques. DIENES (OCDL)
4. L'enfant et les géométries. J. SAUVY (CASTERMANN)
5. Vers l'apprentissage des mathématiques. J. BANDET (COLIN)
6. Initiation mathématique pour les enfants de 5 à 6 ans. DANIAU (CEDIC)
7. Mathématiques et thèmes d'activités. G. BROUSSEAU (HACHETTE)
8. Prémathématique contemporaine. THIRIOUX (MAGNARD)
9. Comment faire les activités math. à l'école maternelle. TOUYAROUT (NATHAN)
10. L'enfant à la découverte de l'espace. J. SAUVY (CASTERMANN)
11. Chemins de découverte mathématiques... L.TOURTET (COLIN)
12. Découverte de la mathématique par les jeux . A. BATBEDAT (L'ECOLE)
13. La naissance de l'intelligence chez l'enfant. J. PIAGET (PUF)
14. La genèse des structures logiques élémentaires. J. PIAGET (PUF)
15. Intuitions et construction de l'espace R.PED.n°78 (INRP)
16. Manipuler, organiser, construire F. BOULE (A.COLIN )
17. Mathématiques en maternelle N° spécial de Grand N (Irem GRENOBLE)
18. Activités mathématiques : G. ZIMMERMANN (NATHAN)
* les apprentissages préscolaires
** le développement cognitif de l'enfant
19. Les mathématiques par les jeux. L. CHAMPDAVOINE (NATHAN)
20. L'enfant et l'espace : le rôle du corps L. LURCAT (PUF)
21. L'activité graphique à l'Ecole Maternelle L. LURCAT (ESF)
22. Apprentissages numériques en maternelle ERMEL (HATIER)
23. L'enfant, le nombre, la numération BOYERA-CAILLERETZ(NATHAN)
24. Jeux logiques et numériques M.L. WINNINGER (RETZ)